Research

Two of my main research areas are sequential decision making problems under uncertainty and qualitative methods in inverse scattering theory.

Sequential Decision Making Problems under Uncertainty

Sequential decision making consists of series of decision and information while incurring costs or receiving rewards. For each $t=0, 1, 2,\ldots, T$, denote the state variable by $s_t$, decision variable by $x_t$, exogeneous information by $w_{t+1}$, transition function by $\mathcal{T}(s_t, x_t, w_{t+1})$ and the contribution function by $c(s_t, x_t)$, the solution of the sequential decision making problem is the best policy $\pi$ with $x_t = x^\pi(s_t)$ and maximizes the cumulative contribution

\[{\sf E}\left\{\left.\sum_{t=0}^T c(s_t, x_t)\right|s_0\right\}\]

Such formulation is ubiquitous in engineering, transportation, healthcare, and finance.

Sequential decision making problems are so diverse that the field has become fragmented into various communities with competing modeling approaches and algorithmic strategies. Quantitative finance problems I have been working on are attributed to the communities of

• stochastic optimal control: asset allocation problem
• optimal stopping problems: Bermudan option pricing; estimation of reinvestment risk in callable bonds
• deep learning and deep reinforcement learning: dynamic hedging of options by deep learning

Currently I am applying the heuristics for sequential decision making problems appeared in the paper to improve the published memory-enhancing spaced repetition algorithm, which is the integral part of my own software solution.

Qualitative Methods in Inverse Scattering Theory

The core problems of scattering theory are the scattering of (time-harmonic) acoustic or electromagnetic waves by penetrable inhomogeneous medium of compact support and by a bounded impenatrable obstacle. The inverse scattering theory is the problem of determining the characteristics of the medium and the obstacle from scattering data, and it has important applications in medical imaging and nondestructive testing.

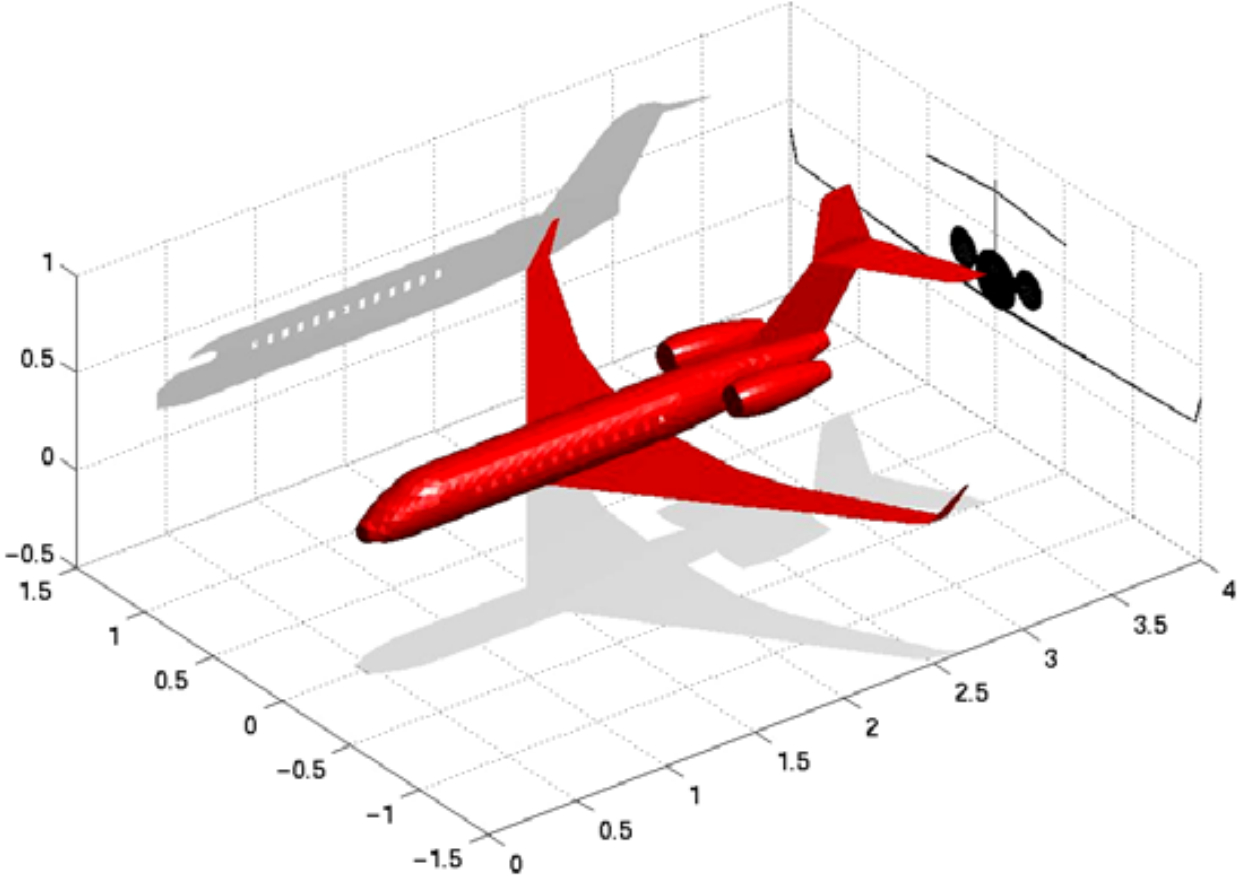
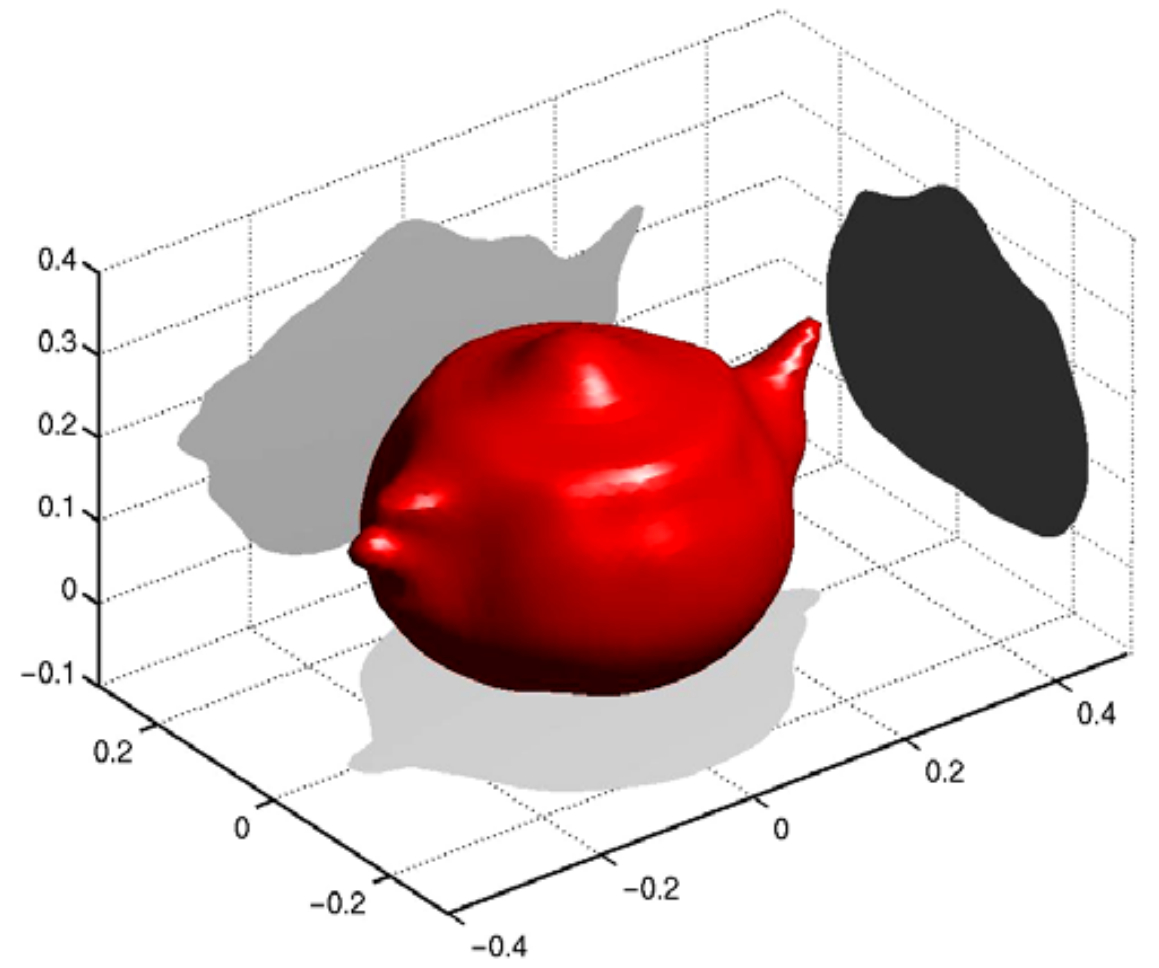
Qualitative methods in inverse scattering theory refer to the collection of methods that avoid weak scattering approximation and nonlinear optimization with a priori information. My studies involve two of the most prominent methods, namely the linear sampling method and the factorization method. Using the linear sampling method, reconstruction results of an airplane and a teapot from far field scattering patterns are shown in above figures. I have been working on the open problem of applying the factorization method to perfect conductors; papers in the repository summarize my latest attempts.